Экстремальная задача
Точно поставленная экстремальная задача включает в себя следующие элементы: функционал (в теории экстремальных задач числовые функции часто называют функционалами) 
, определенный на некотором множестве X, и ограничение, т.е. некоторое подмножество 
(через 
обозначается совокупность всех вещественных чисел, пополненная значениями 
и 
). При этом сама задача формулируется так: найти экстремум (т.е. верхнюю или нижнюю грань) функционала f при условии, что 
. Одним из классов в теории экстремальных задач является класс гладких задач с ограничениями типа равенств и неравенств:
при этом класс допустимых элементов X обычно нормированное пространство, ограничение C задается равенством 
, где 
– отображение X в другое нормированное пространство Y, и конечным числом неравенств 
Для решения подобных и других задач используется метод множителей Лагранжа.
Одним из вариантов использования экстремальных принципов является метод, при котором стационарное состояние некоторого биологического объекта описывается как решение задачи на условный экстремум вида
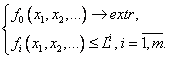
Здесь 
— некоторые фазовые переменные, описывающие состояние исследуемого объекта, 
— некоторая целевая функция (или функционал в более общем случае), 
— функция состояния и 
— известные характеристики объекта, 
. Ограничения 
обычно имеют смысл либо законов сохранения, либо прямо следуют из природы задачи.
П. В. Фурсова
Литература:
Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление. М.: Наука, 1979. 429c